
APA Style
Yemi Taiwo, Oladimeji Ismaila, Adebisi Baale, Olufemi Awodoye, Isiak Adeyemo, Temitope Taiwo, Oluwatosin Taiwo, Adeoluwa Taiwo, Muibat Ismaila. (2025). An Enhanced Puma Optimized Reinforcement Learning Model for Detection of Results Anomalies in Higher Education. Computing&AI Connect, 2 (Article ID: 0020). https://doi.org/10.69709/CAIC.2025.190984MLA Style
Yemi Taiwo, Oladimeji Ismaila, Adebisi Baale, Olufemi Awodoye, Isiak Adeyemo, Temitope Taiwo, Oluwatosin Taiwo, Adeoluwa Taiwo, Muibat Ismaila. "An Enhanced Puma Optimized Reinforcement Learning Model for Detection of Results Anomalies in Higher Education". Computing&AI Connect, vol. 2, 2025, Article ID: 0020, https://doi.org/10.69709/CAIC.2025.190984.Chicago Style
Yemi Taiwo, Oladimeji Ismaila, Adebisi Baale, Olufemi Awodoye, Isiak Adeyemo, Temitope Taiwo, Oluwatosin Taiwo, Adeoluwa Taiwo, Muibat Ismaila. 2025. "An Enhanced Puma Optimized Reinforcement Learning Model for Detection of Results Anomalies in Higher Education." Computing&AI Connect 2 (2025): 0020. https://doi.org/10.69709/CAIC.2025.190984.
 ACCESS
Research Article
ACCESS
Research Article
Volume 2, Article ID: 2025.0020

Yemi Taiwo
yemsrtad@gmail.com

Oladimeji Ismaila
woismaila@lautech.edu.ng

Adebisi Baale
aabaale@lautech.edu.ng

Olufemi Awodoye
ooawodoye50@lautech.edu.ng

Isiak Adeyemo
iaadyemo22@lautech.edu.ng

Temitope Taiwo
themmy.t@outlook.com

Oluwatosin Taiwo
ta.oluwatosin@gmail.com

Adeoluwa Taiwo

Muibat Ismaila
folaismaila@gmail.com
1 Department of Computer Science, Faculty of Computing and Informatics, Ladoke Akintola University of Technology, Ogbomoso 210214, Nigeria
2 Department of Information Systems, Faculty of Computing and Informatics, Ladoke Akintola University of Technology, Ogbomoso 210214, Nigeria
3 Department of Computer Engineering, Faculty of Engineering and Technology, Ladoke Akintola University of Technology, Ogbomoso 210214, Nigeria
4 Department of Computer Science, College of Science and Technology, Covenant University, Ota 112233, Nigeria
5 Department of Electrical & Information Engineering, College of Engineering, Covenant University, Ota 112233, Nigeria
6 Department of Computer Science, Faculty of Information and Communication Technology, Kwara State University, Malete 241103, Nigeria
7 Department of Mathematics & Computer Science, Fountain University, Osogbo 230211, Nigeria
* Author to whom correspondence should be addressed
Received: 27 Apr 2025 Accepted: 27 Jul 2025 Available Online: 28 Jul 2025 Published: 08 Aug 2025
The integrity of a degree depends on the accuracy and validity of examination results, which must be carefully processed and protected. The number of students being admitted to Nigerian higher education is rising yearly, making it harder for existing legacy infrastructure and the limited workforce to handle the resulting processing abnormalities. This typically leads to a significant delay in approving student results for subsequent decision-making. Unauthorized result manipulations is a common occurrence in higher education settings, and often serve as precursors to certificate counterfeiting. Given the critical role of exam administration in educational management, appropriate technologies are needed to ensure process effectiveness. Ensuring the accuracy and integrity of educational certificates and consequently preventing certificate forgery, requires that anomaly detection phase be built into result processing systems. Therefore, blockchain technology was integrated with an enhanced Puma-optimized reinforcement learning algorithm, to develop a secure and intelligent system for result filtration, storage, and protection. This platform utilized an enhanced Puma-optimized reinforcement learning algorithm in a Q-learning architecture for real-time anomaly detection. The resulting architecture was further fused with the traditional security features of blockchain technology, specifically its immutable and distributed ledger, through design, training, and testing simulations conducted in MATLAB. The improved reinforcement learning agent used a quantum superposition mutation operator to enhance the optimization process to achieve high efficiency, filtering out anomalous results in real time. To avoid local optima traps, balance exploration and exploitation, and guarantee diversity in the search for optimal parameters, the operator introduced controlled randomness. Accuracy, Precision, False Positive Rate, F1-Score, Specificity, Recall, and Detection Time were used to compare the performance of the enhanced model with those of traditional reinforcement learning, standard Puma-optimized reinforcement learning, and existing state-of-the-art works. With a 0.47% false positive rate, 99.53% specificity, 98.11% precision, 97.33% recall, 99.09% accuracy, and 42.38 milliseconds computation time across 800 epochs, the model demonstrated a high level of efficiency in detecting anomalies in students’ results.
The security vulnerabilities of traditional database systems, the increasingly volatile information security landscape, and the inadequacy of traditional data security measures, necessitated a new, better, and integrated approach to data security. Educational institutions are susceptible to the security issue, as existing record-keeping systems in higher education have left much to be desired, particularly in terms of data security [1]. Ideally, a comprehensive data security policy requires a careful blend of user education, encryption systems, access control measures, threat detection and prevention mechanisms, and physical protection. When a pattern that does not show a well-defined regular behaviour is observed during the communication process or in application data, an anomaly is suspected [2]. According to Zimek and Erich [3], abnormality detection involves identifying unusual data, patterns, observations, or occurrences that are suspicious because they differ noticeably from the bulk of the data and typical system or user behaviours. Anomalies may include data errors, structural flaws, or behavioral deviations. They can also be in the form of noise, outliers, or novelty. While intrusion detection focuses on monitoring network traffic and devices to identify malicious patterns or events, anomaly detection utilizes machine learning algorithms to detect behavioral or transactional patterns that deviate from the norm. A modern approach to data security integrates machine learning for predictive analytics [4] and blockchain for decentralized, immutable storage. Various techniques have been used to implement data security in host-based and distributed applications, ranging from data mining to rule-based approaches and presently machine learning. The first technique used was data mining, which simply involves extracting patterns out of the knowledge collected from a robust knowledge base and using those patterns to identify abnormalities within related data [5]. The rule-based approach creates a database of the signatures of known abnormalities for use in determining if any data transaction or behaviour is abnormal or not. These approaches were incapable of identifying new patterns or behaviours that use new signatures, since such new signatures may not be in their knowledge bases. Machine Learning (ML) was introduced into the data security equation to yield intelligent monitoring systems that can learn patterns from the underlying application data, making them capable of detecting any unusual patterns or behaviours, and reporting such anomalies. ML is increasingly being embraced, particularly in the design and implementation of secure and integrated distributed information platforms. Several techniques have been used to identify anomalies, especially in systems that are host-based. Distributed systems, which are more complex and of intricate topologies, haven’t really benefited from this, most likely because of their intricate structural dependencies. Architectures like K-Nearest Neighbours [6], Deep Boltzmann Machine/Generative Adversarial Networks [7], Deep Neural Networks [8], and Deep Belief Network [9], are examples of machine learning techniques that have been used for implementing both intrusion and anomaly detection. However, the choice of Reinforcement Learning in this study is driven by its growing adoption among researchers, owing to the significant benefits it offers. A reinforcement learning agent is usually designed to operate on the principle of learning from the interaction with its environment through the feedback it gets when it takes an action on the environment [10], using architectures like Q-Learning, Deep Q-Learning, and Model-Based Value Estimation etc. Aside from its ability to yield highly accurate predictions, reinforcement learning agents have faster computation time compared to alternative models [11], and do not require large labelled datasets, thereby optimizing the use of resources like storage, primary memory, and processor cycles. Aside from being ideal for tasks involving a sequential decision-making process, it is also innovative as it can yield new solutions to problems, even beyond those envisaged by humans, hence it is considered the future of machine learning. Since a reinforcement learning algorithm does not need retraining to adapt to similar environments, it can save time and cost. To address the challenge of unauthorized result manipulation in educational institutions, researchers have proposed using blockchain technology as a more secure and reliable alternative to conventional databases for storing academic records. Although the technology has advanced in other domains, its adoption in education is still in its infancy. Aside from the technology’s immutability feature, which makes it irrevocable, it is also distributive and validated, providing a better solution to the data security problem [12,13]. However, advancements in Information and Communication Technology brought a matching sophistication in the tools and techniques available to hackers, making blockchain technology susceptible to anomalies. The current trend of combining machine learning with blockchain technology is a direct effort to improve data security through integrated, intelligent, and proactive systems that can think and act like human experts. Research on data security is a continuous process as demanded by the ever-dynamic nature of ICT and the complexities of its application domains. Such a process emphasizes the combination of machine learning with other AI-compatible technologies. Irrespective of the application domain, machine learning techniques can be developed to scrutinize incoming results to uncover abnormalities, enable real-time detection of unusual results, prevent such from being recorded into the blockchain storage, allow administrators to act swiftly, minimize attacks, and reduce the risk of theft of academic records. This research aims to develop an integrated platform that combines blockchain technology with a reinforcement learning agent to monitor examination results in higher education institutions. Section 2 reviews related studies on result anomaly detection. While Section 3 details the specific approaches, techniques, and data utilized for the study, Section 4 presents and discusses the results of applying both techniques and data to the identified problem. Section 5 details the inferences that were drawn from the entire study, while Section 6 presents authors’ recommendations.
Notwithstanding the significant progress that has been made by researchers on the application of artificial neural networks to real-world machine learning problems, the use of machine learning-based techniques for detecting anomalies in examination results within the education domain is relatively in its infancy, and as such, existing works are also scarce [14]. However, some anomaly detection studies in other domains that are considered relevant to this work were reviewed. Existing Studies Initial efforts at anomaly detection were focused on the activities of insiders. Some studies attempted to understand why insiders act in certain ways by using theories of decision-making and psychological models. For example, authors in [15] provided an approach for modeling the insider threat based on behavioral and psychological insights. By employing an analytical construct based on the model, an analyst can create hypothesis trees defining possible insider threats from metrics in several areas, such as individual conduct and organizational policy. In their study, Rashid et al. [16] took each user’s weekly routine to look for variances that may indicate insider anomalies using a Hidden Markov Model (HMM). The HMM is a mathematical tool in which all hidden state emit a symbol from a range of possible values before changing to a new one. This worked well for modeling typical behaviors that are derived via sequential data mining. Users’ log-likelihood for the new action set is computed after training the model, so it can represent users’ action sequences over a certain amount of time. The sequence is marked as anomalous for further research when the log-likelihood score exceeds a threshold. The action series is paired with the previous action sequence to retrain the HMM, if not flagged or if the analyst clears the flag. A more accurate and efficient approach is to model the normality in either network traffic behaviours or transactional data patterns, and use it as a standard to identify anomalies, being deviations from the baseline or modeled normality. Therefore, a number of machine learning-based anomaly detection systems have been implemented by scholars, each with its strengths and weaknesses. A visual analytical system involving the collection of statistics from Ethereum was proposed in [17]. The model transformed the collected information into a chronological dashboard for visualization, demonstrating that the data enabled the detection of the DAO attack by highlighting anomalous peaks occurring near the corresponding date. The objective is to provide a visualization tool that can be easily used by non-technical personnel to identify potential anomalies in blockchain transactions. An anomaly detection system called PRODIGAL was introduced, supported by the Defense Advanced Research Projects Agency (DARPA), which integrates various anomaly detection techniques that utilize machine learning to support human experts [18]. The need for high-speed anomaly detection at the network layer of a blockchain was advocated in [19], to prevent malicious transactions from getting recorded in the immutable ledger. They detailed issues that can result from malicious transactions being recorded on a blockchain before detection. They offered a model that uses a k-means algorithm to identify anomalous data, an accelerated process that ensures both anomaly detection and feature extraction are done in the GPU memory. The GPU-based model was claimed to be 37.1 times faster than traditional CPU-based models. It was also compared against those of GPU-based models that do not execute feature extraction on a GPU, and was reported to be 16.1 times quicker. They asserted that so far, entropy in networks has only been studied using clustering-based models, and that there is a need for improved techniques like reinforcement learning and deep learning. A dual machine learning architecture was proposed in [20], utilizing a One Class Support Vector Machine (OCSVM) algorithm to identify anomalies and a K-means algorithm for grouping similar anomalies. The study focused only on detecting anomalies in bitcoin transactions by making a dataset containing a set of normal bitcoin transactions as the basis of their model design. Using the same bitcoin transaction dataset, they created another dataset cataloguing bitcoin transaction-based attacks. Blockchain Anomaly Detection (BAD) was suggested by [21] as a system that gathers data from both the orphan and the mainchain blocks. Their approach of storing data about each branch taking place on the blockchain could make the large volume of data generated difficult to manage. Also, it requires modification of the protocol since its design does not allow the storage of information concerning orphan or branch blocks. Authors in [22] proposed an encoder-decoder model, which employed the data gathered by a blockchain’s operations, to identify anomalies in the underlying network traffic that may indicate an impending or ongoing attack. The research determines a set of attributes that may be calculated from the blockchain logs to characterize the system’s state at each time step. They also added an unsupervised neural architecture that can calculate a score that indicates the extent of anomaly displayed by a time series, indicating the network’s condition in a given period. The main drawback with their approach was the limited events to classify because of the limited amount of blockchain transactions that were used for training the model in an unsupervised approach. For instance, their model highlighted a serious anomaly on day 1255, which was a few days after the actual attack. Also, their approach utilized block size and its associated features as the base dataset, by excluding data from other sources like servers, operating systems, and applications. This limited the model’s effectiveness in early detection of certain attack types. A Feed-Forward Neural Network model was proposed by [23] for the detection of result anomalies in higher education. The proposed architecture has two input variables corresponding to continuous assessment and examination scores, a hidden layer, and two output layers of continuous assessment and examination anomalies, respectively. The study utilized a weighted continuous assessment value as a benchmark for detecting abnormal data points, categorizing them into the rejected region. An object-oriented analysis and design approach was adopted for defining either the static or dynamic context of the model, and for designing the system architecture into layers and subsystems. An architecture that collects Bitcoin transactions data via Google for use as a dataset was proposed in [24], with sender names as captions. Deep features are extracted from transactions in the dataset, and label refinement is done in addition to the creation of a suggestion list. Identification of unusual patterns or behaviour was achieved using a supervised Support Vector Machine network to classify blockchain transactions into normal/anomaly, and then use the suggestion list for the tagging. A framework that employed Support Vector Machine (SVM) and K-Nearest Neighbour (KNN) algorithms for detecting interference in a blockchain-based network was proposed by [25]. The study utilized IoT technology to collect data from several cloud environments, for onward transmission to the data pre-processing layer and eventual storage in blockchain-secured clouds. The model proposed in the study uses machine learning algorithms, and adopts blockchain for the storage of the dataset in order to ensure the security of both trained models and pre-processed data. Further, authors in [26] used an integrated architecture of Long Short-Term Memory (LSTM), Gated Recurrent Units (GRU), and a blockchain to create a privacy-preserving anomaly detection framework. It used blockchain to safely transmit data to a distributed, decentralized cloud server for local model training using federated learning. Focusing on the NSL-KDD dataset, the study used various storage techniques to ensure data safety and confidentiality, using blockchain, federated, and hybrid learning to solve privacy concerns and promote free collaboration. Using federated learning leaves the training open to inference attacks through data leakage. The efficiency of the training process could be hampered by latency in network communication, particularly during transmission and aggregation of model updates. GraphAEAtt, a self-encoder system with an attention mechanism and, deep learning framework, was introduced in [27] for blockchain abnormal transaction detection. It comprises an attribute autoencoder and a structural autoencoder that work together to jointly learn node and attribute feature vector representations, with an attention mechanism to learn the correlation between adjacent nodes. After the observed raw node attributes are first transformed into a vector representation of the low-dimensional space by the structural encoder, all surrounding nodes’ embeddings are combined to create the node integration using the shared attention technique. The observed attribute data is then mapped into a hypothetical attribute embedding form by the attribute encoder using a multi-layer perceptron. The adjacency matrix is reconstructed using a structure decoder, while the attribute matrix is reconstructed using an attribute decoder, after which the objective function for the model training is measured as the nodes’ reconstruction error. The reconstruction inaccuracy of the nodes is used for the anomaly detection. Research Gap Previous studies focused on supervised learning algorithms optimized using learned optimizers [28], despite the potential benefits of developing new adaptive optimizers [29]. This has, over time, resulted in models with high computation (detection) time, low accuracy, and high false alarms. In addition, the creation and training of learned optimizers typically requires a significant amount of computation and human labour, due to their intricate neural architecture and inclusion of multiple hand-designed input features. Also, learned optimizers have been found to perform poorly on even simple reinforcement learning tasks [28,30]. Although learned optimizers were able to detect a number of abnormalities in data, their effectiveness at detection needs to be improved. Such improvement efforts or research should focus on enhancing existing deep learning techniques or developing new reinforcement learning techniques [31,32]. This study addresses the above shortcomings by formulating an adaptive optimizer to enhance a reinforcement learning-based anomaly detection architecture.
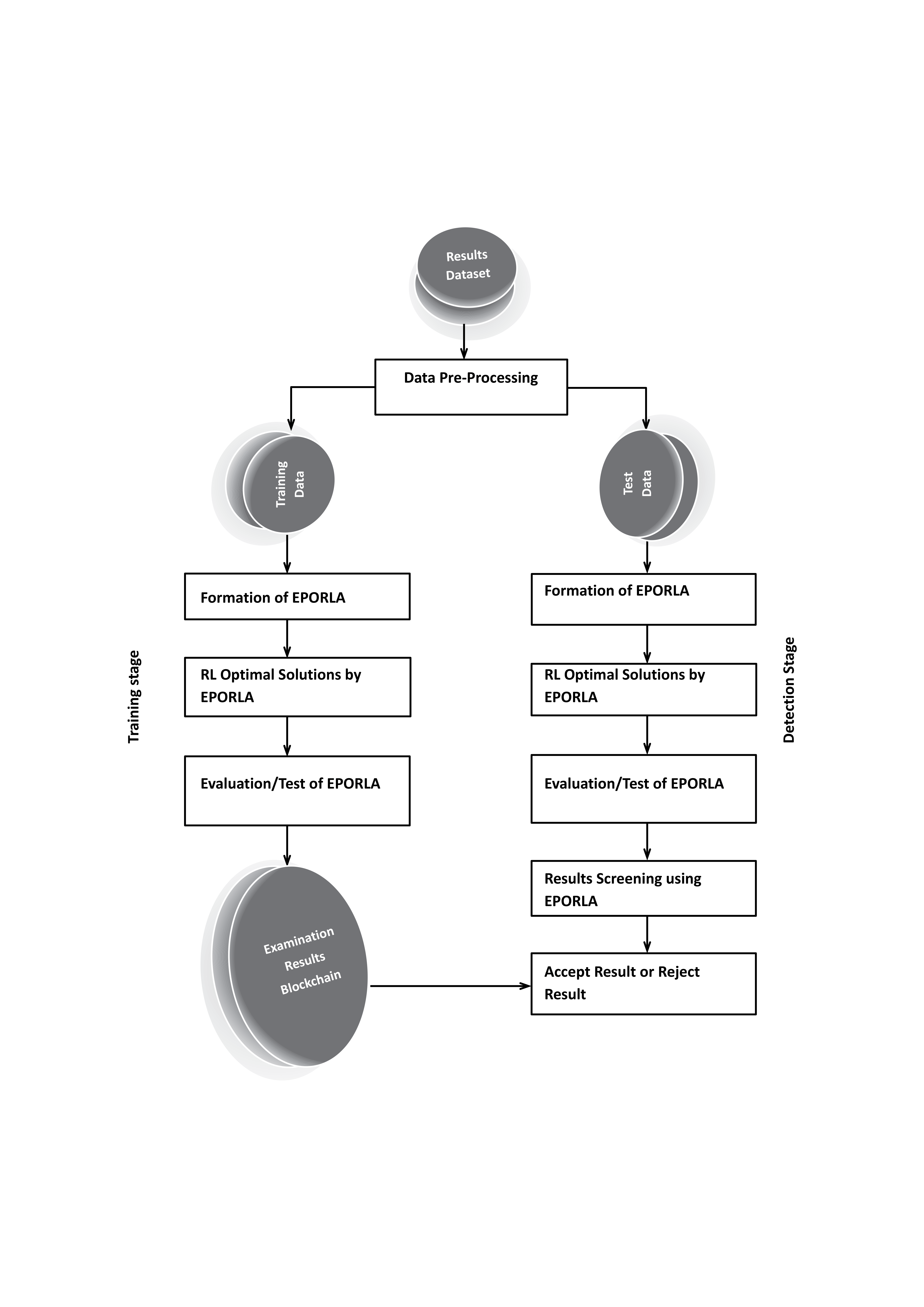
In addition to formulating an enhanced Puma optimized reinforcement learning algorithm (EPORLA), a blockchain network was built to provide an integrated, intelligent, and adaptive examination results filtering system that is also capable of predictive analytics. The enhanced Puma optimizer was formulated in a manner that it returns the optimal set of values for the reinforcement learning hyperparameters within a few iterations. The enhanced reinforcement learning algorithm and the blockchain network were designed in MATLAB (R2023a). Alternatively, these two main components can also be simulated using either Java or Python, taking advantage of their rich toolboxes and libraries. The effectiveness of the developed model in filtering examination results of anomalies was measured using Accuracy, Precision, Recall, False Positive Rate, F1-Score, Specificity, and Computation Time. Model performance, findings, and experimental data are discussed, while findings and experimental data were also presented. The framework and flowchart detailing the operational components and flow of activities in the result anomaly detection system are illustrated in Figure 1 and Figure 2, respectively. Dataset Sample examination results of about 6238 students across 100 to 500 levels of various academic programmes were obtained from the record office of Ladoke Akintola University of Technology, Ogbomoso. Data Preprocessing The data used for training and validating the Puma-optimized reinforcement learning agent were preprocessed to ensure feature alignment, eliminate ambiguity, and provide the algorithm with clean, noise-free input. Preprocessing was necessary because the availability of required features in a dataset can assist in closing the gap between academic research and real-world implementation of machine learning-based applications, by enabling a more rigorous and comprehensive evaluation of such systems [33]. Also, the performance of any machine learning algorithm is heavily dependent on the quality of the data. Data Merging and Integration: Since raw examination results were obtained for students at different levels of various academic programmes, there were multiple Comma Separated Values (CSV) files containing datapoints corresponding to sample examination results. Each CSV file contains sample examination results for all students taking any particular course at any particular level of a programme. For example, the results of all 100 Level Computer Science students in Data Structure (CSC 102) were kept in a separate CSV file. The initial raw dataset for the study was created by merging all data points from the various acquired examination result CSV files into a single consolidated CSV file. Data Reduction: In this phase, emphasis was placed on dimensionality reduction by deleting from the raw CSV datafile features considered less important to the task at hand. First, doing this ensures the RL algorithm, like other machine learning architectures, works efficiently with fewer features in the final dataset, avoiding the curse of dimensionality. Second, it helped ensure a coherent and understandable model due to a smaller number of features, avoiding structural complexity. Third, the reduced number of features allowed the RL model to optimize the use of computing resources like secondary storage, primary memory, and processor cycle time. Features such as Student Name, Course Description, Credit Unit, Semester, etc., were manually deleted, leaving Matric, Level, Course Code, Score, and Date Timestamp. Data Cleaning and Insertion: Denoising the reduced data file is necessary to present the learning algorithm with a clean dataset. For example, columns with missing values were treated by computing the Missing Value Ratio (Rm). An entire feature (column) is removed from the dataset if the missing rate (Rm) is significantly high; otherwise, missing values are imputed using the mean, median, or mode of the respective column. To ensure effective model training and validation, at least a row of anomalous results was manually inserted into the dataset for every ten rows of non-anomalous results. Specific activities carried out to achieve the ideal dataset are as follows: i. One-valued columns (i.e., those with all zero values) were deleted. Columns with zero values throughout. Such columns do not have any influence on the output. ii. Also, one-valued rows (rows with zero values throughout) were deleted. iii. Datapoints (rows) with negative values throughout were also deleted. iv. Missing values were treated by computing the Missing Value Ratio for affected columns. v. Columns (features) already known to be irrelevant to the task at hand were removed. vi. A total of 568 anomalous samples were generated using MATLAB’s randn() function, based on the mean and standard deviation of the normal data. An offset was applied to shift the mean, combined with numeric assignment, to ensure that the generated samples deviated by several standard deviations from the normal mean, thereby producing extreme anomalies. Thereafter, every ten rows of normal results have one anomalous sample manually inserted from the generated anomalous samples. vii. A column tagged “Status” was created as the last column to serve as the label for each datapoint. Data Splitting: The resultant dataset from (3) above was divided into two samples in a ratio of 7:3 corresponding to training and validation subsets, respectively, using a random subsampling cross-validation method. Components Initialization The first major phase in implementing the proposed examination results anomaly detection system involves the initialization of key blockchain and reinforcement learning components. The blockchain network was initialized by defining nodes and a Proof-of-Authority (PoA) consensus mechanism. Smart contracts were also designed to provide a mechanism for validating examination results. The genesis block, which carries no real-world transactional data, was defined as a store of the foundational rules or generic block format, from which successive data blocks in the blockchain propagate. Data block configuration was done to store only sensitive data fields of students’ examination results. Successive data blocks were cryptographically linked together using the SHA-256 hashing algorithm to form an immutable ledger. The blockchain provides the required decentralized storage infrastructure, transparency, and trust for the examination results system. The operation of the enhanced reinforcement learning algorithm is initialized by first defining core components like States, Actions, Rewards, and the Q-table. This setup enables the RL agent to dynamically learn optimal strategies for scrutinizing incoming data to identify any abnormality. The RL environment and operational variables were defined as follows: S: set of states that are equated to stages of result verification, such as “Pending Verification”, “Valid Entry”, or “Malicious Entry”. A: actions set that includes operations such as “Store Result” or “Reject Result”.
: The reward function that incentivizes correct abnormality detection and penalizes detection errors.
: Q-table that the RL agent utilizes to initialize state-action pairs with random values. Sets hyperparameters such as the learning rate (α) and discount factor (γ). Model Optimization The reinforcement learning algorithm was positioned for maximum efficiency and accuracy of detection by ensuring that required adjustments to its parameters and the eventual determination of the optimal set of parameters that guarantees the lowest possible loss were done using Enhanced Puma Optimization Algorithm (EPOA) that is integrated with Quantum Superposition Mutation (QSM). EPOA-QSM provides an intelligent and completely automatic phase switching mechanism for achieving a balance between exploration and exploitation, enhances exploration by incorporating quantum-inspired randomness, and prevents solutions from settling into suboptimal local minima. It ensures the model is trained most efficiently by selecting an optimal set of parameters that guarantees the shortest possible training time; an essential service as the choice of hyperparameters can greatly impact the model’s performance. The iterative process of parameter optimization continues until fitness evaluation indicates no significant improvement in fitness scores, with the model having reached convergence. Parameter optimization starts with the algorithm generating a random set of N populations Xi, including the discount factor, learning rate, and Q-values. Computation of the fitness evaluation score—F(Xi), is done for the individual combination of parameters Xi by comparing the ground truth with the prediction using a loss function.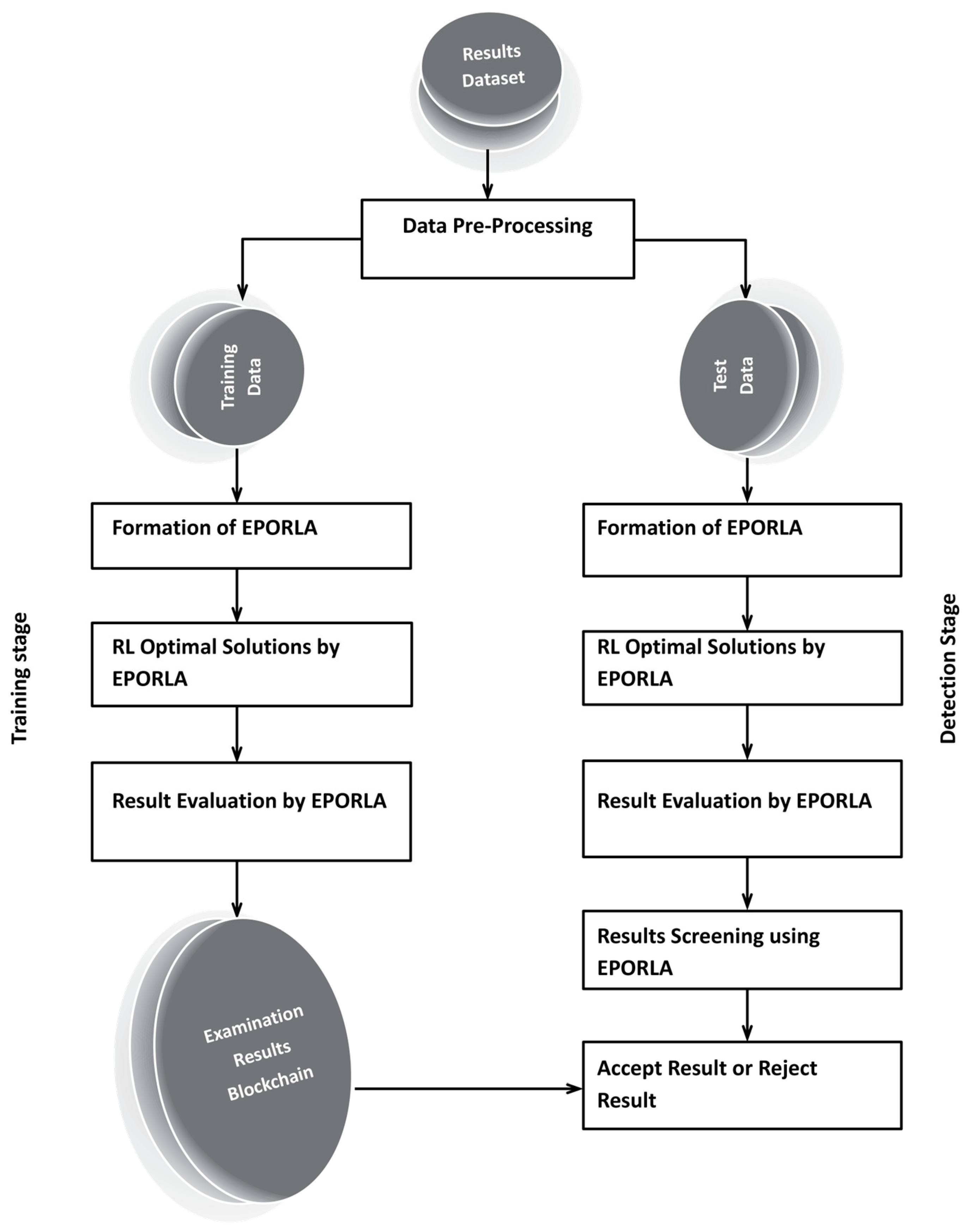
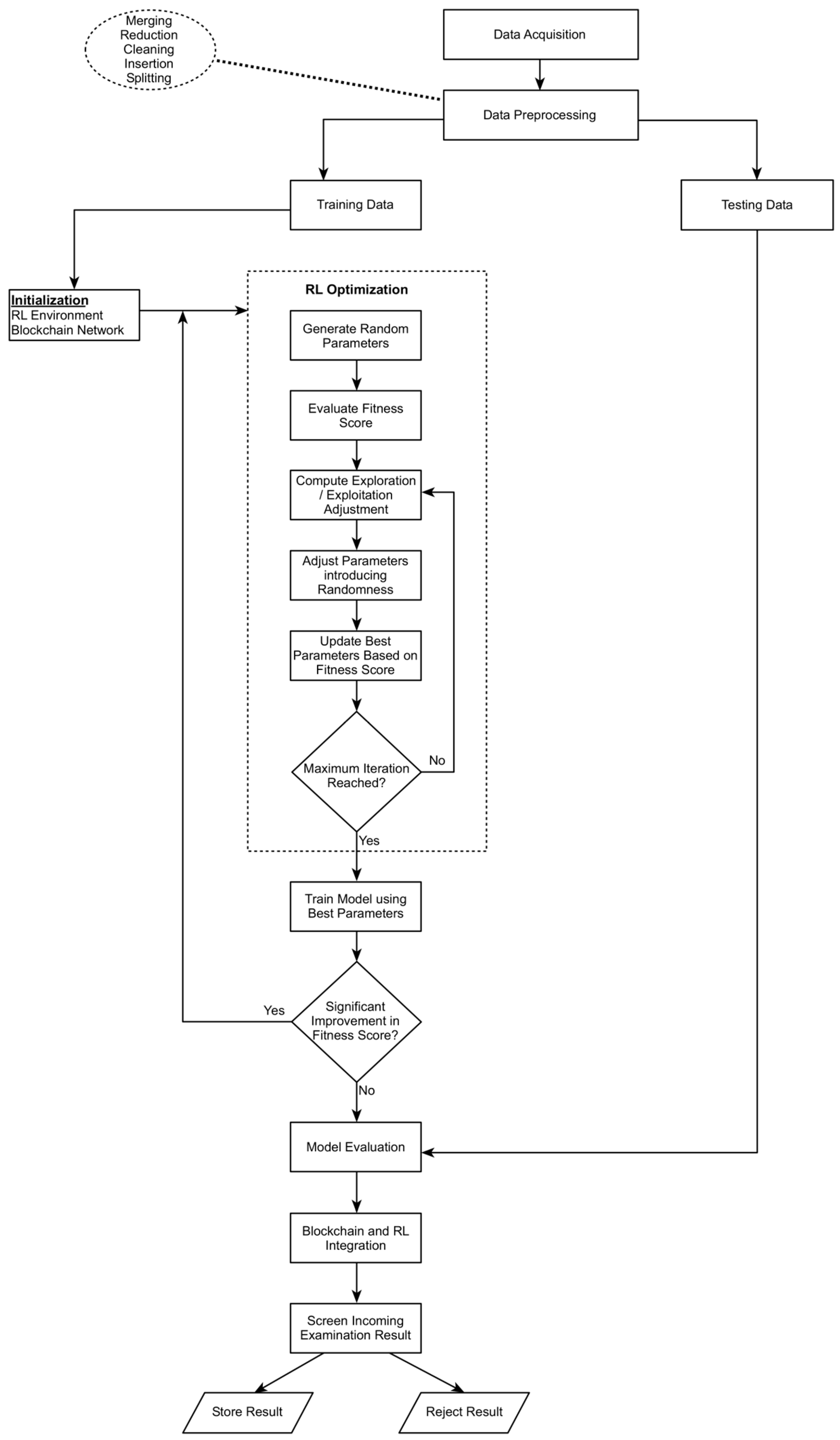
The fitness score is useful for determining how accurate the chosen parameters are in aiding the model’s effectiveness in detecting malicious results. To prevent the process from converging to a local optimum, which may happen when only one particular phase is repeatedly selected over many iterations, the phase selection was diversified. Such diversity was achieved through the controlled randomness introduced into the optimization process by the integrated QSM operator. EPOA-QSM also ensures that any phase that has not been selected in many iterations of the optimization process also stands a chance of being selected. As a result, EPOA-QSM was able to avoid stagnation, make provision for automatic parameters selection and continuously improve solution quality, ensuring a more robust reinforcement learning model.
For
to
Exploration (Quantum Enhanced Prey Search)
Exploitation (Quantum-Inspired Hunting)
Parameters Selection
Model Training
The training phase commenced immediately after the reinforcement learning parameters were optimized. In the course of training, optimized parameters were applied to real-world examination results, with the EPORLA observing the current state for each transaction, and then deciding on an action based on either exploitation (learned Q-values) or exploration. Thereafter, reward R (St, At) was estimated based on the corresponding feedback from the action taken. The model over time improved its decision-making by utilizing the feedback loop to update the Q-values.
EPORLA iterative optimization, training, blockchain integration, and anomaly detection procedure is outlined in Algorithm 1.
| Algorithm 1: Enhanced RL-Based Examination Results Anomaly Detection | |
| //Input: Results Dataset:
, where Blockchain Network: Optimization Parameters: Population size exploration factor ( ), exploitation factor ( RL Parameters: State space , action space //Output: Optimized RL parameters, blockchain of results, result status Create network: Define nodes and consensus mechanism, Develop smart contracts for validation rules and block storage, Create Genesis block: Initialize blockchain and validation rules. Define RL Variables: Actions as set A = {“Valid “, “Reject”} State as set S = {“Pending”, “Valid”, “Malicious”} Reward Function as Set initial values for all state-action pairs: . Set hyperparameters: learning rate Generate Compute the fitness of each . for Exploration phase: Calculate exploration adjustment Exploitation Phase: Adjust solutions using set parameters Training Phase: Observe state for result ( Choose action using Calculate reward ). Update Q-values using Blockchain Integration: if RL approves result ( ) then validate and store else report as anomalous and log it for further review endif if no significant improvement in fitness score, then t endif next t End |
Anomaly Detection
The reinforcement learning model makes decisions regarding anomalies based on the training it has received in subsection E above. The incoming result is passed to EPORLA, which scrutinizes it to determine whether it is of the expected pattern, as may be inherent in the bulk of the examination results, or a deviation. If considered to be of the expected pattern, it is propagated to the participating nodes for validation. However, if EPORLA considers such an incoming result to be suspicious or abnormal, it flags it as anomalous and prevents it from being propagated to the participating nodes. Such examination results data is submitted for further review. This approach helps ensure that participating nodes do not waste available limited computing resources to validate malicious data.
Blockchain and RL Integration
With the blockchain class and its methods, tasks such as the addition of data blocks, chain validation, and proof of authority computation were accomplished. Participating nodes on the blockchain network were responsible for validating incoming examination results, utilizing the Proof of Authority (PoA) consensus mechanism for ensuring that agreement is reached before recording them to the blockchain’s ledger.
Security and Privacy Protection
The blockchain component was designed as a private blockchain with its access control mechanism tied to the university’s main portal access control policies that must have been defined at both the user and module levels. The EPORLA component of a university result processing system can only be accessed by lecturers or instructors uploading student results. Also, successive data blocks were cryptographically linked together using the SHA-256 hashing algorithm to form an immutable ledger. The AES algorithm, because of its low technical requirements, which make it a faster and more efficient encryption algorithm for handling massive data than the RSA, and also because of its relative flexible implementation on consumer computing devices like laptops and smartphones, was used for encrypting the potentially enormous blocks of data the blockchain is expected to store as it grows.
Model Implementation
The developed technique was implemented in MATLAB R2023a with multiple toolboxes to ensure efficiency and accuracy. The Reinforcement Learning Toolbox was used to develop and train the reinforcement learning model for optimizing result filtration. Additionally, the Blockchain Toolbox was integrated to simulate decentralized ledger operations for secure and immutable storage of examination results, and the Optimization Toolbox was deployed in support of the Puma-based optimization process to improve decision-making and transaction efficiency. The system was implemented on a 64-bit Windows 11 machine with a minimum Intel Core i7 processor, 16 GB RAM, and an NVIDIA GPU for accelerated computations.
Deployment, Maintenance, and User Training
Designed as a full-fledged point anomaly detection tool, the model is not a standalone result processing system on its own. It can only be deployed as an integrated tool or a modular component for anomaly detection within a larger result processing system. A pilot implementation approach can be adopted by institutions deploying the tool to evaluate its effectiveness and compatibility with existing result processing legacy infrastructure. With the construction of blockchain data blocks from only a sensitive and limited number of fields, in addition to the impressive computation time of 42.38 ms, EPORLA is considered scalable and ideal for real-time deployment. The user’s contact with the model is limited to a few selection buttons on the main GUI. Its use requires minimal training, including data upload, classifier selection, parameter settings (such as training percentage and number of epochs), and specifying the output data file destination. As an integrated tool utilizing the base examination results as its operational data, the model requires no special maintenance, more so that it renews itself on the go, being a reinforcement learning-based system.
Model Evaluation
The data for this study is of high class-imbalance since the bulk of it is of normal results, while a smaller percentage of it was configured to be abnormal results. This makes evaluation metrics such as Confusion Matrix, Accuracy, Precision, False Positive Rate (FPR), Specificity, F1-Score, and Recall ideal for evaluating the performance of the system. These metrics were used to measure the system’s effectiveness and suitability in identifying transactional abnormalities in examination results. Considering the huge amount of transactional data that can be generated in a college, these metrics were used to analyze how efficiently the system is in detecting anomalies like unusual data size, wrong data type, and abnormal data pattern. Also, EPORLA’s convergence rate was compared with that of the standard Puma-optimized reinforcement learning algorithm (PORLA).
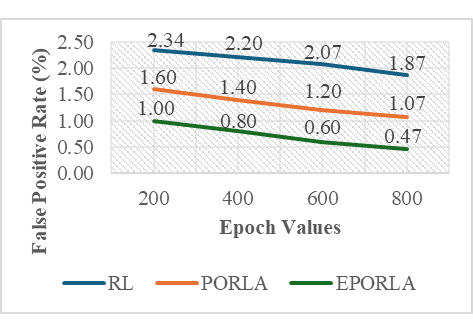
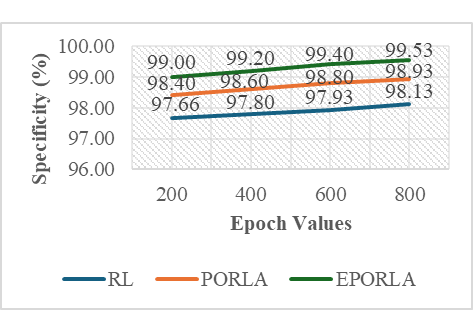
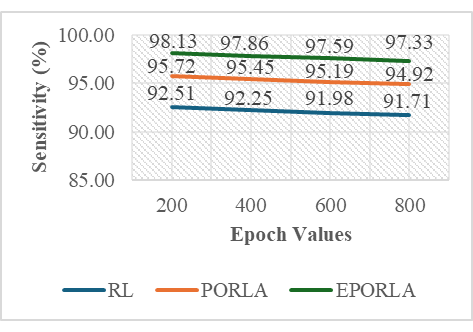
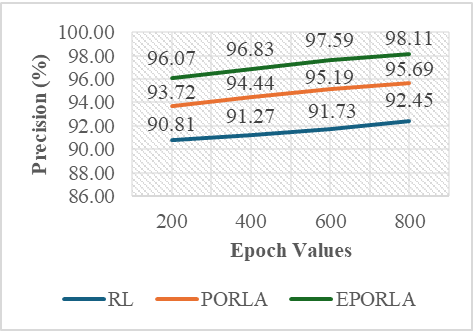
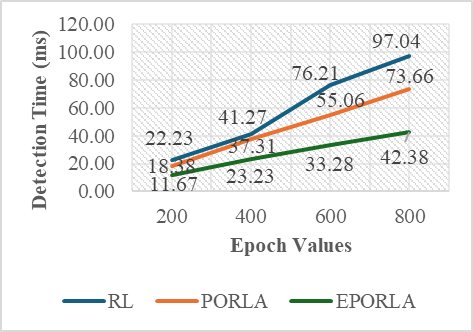
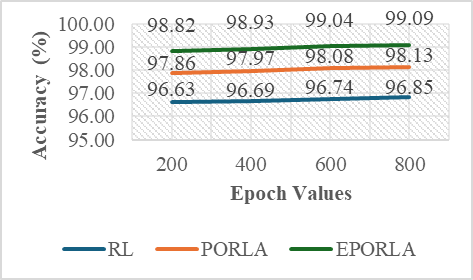
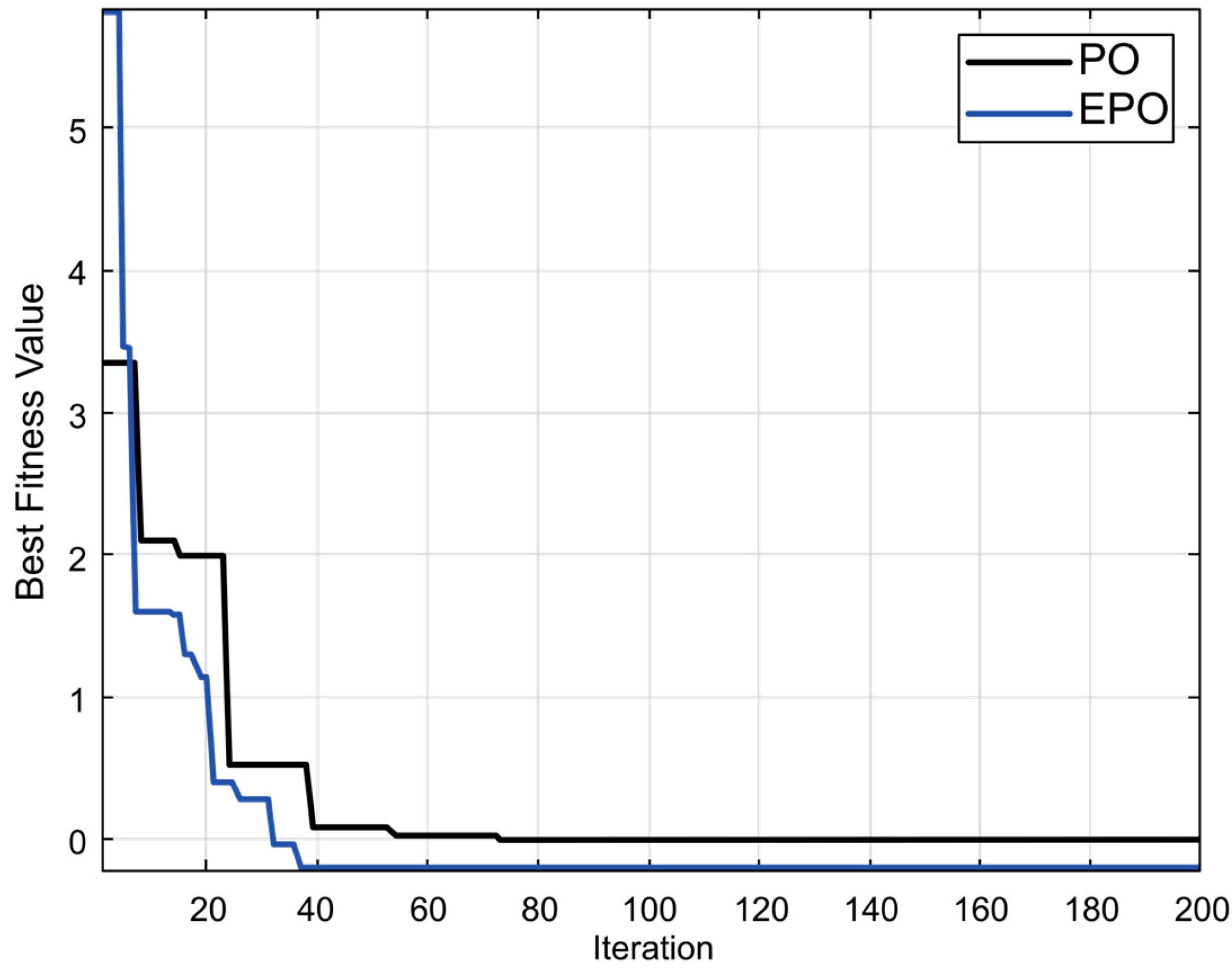
The application of traditional Reinforcement Learning (RL), Puma Optimized Reinforcement Learning Algorithm (PORLA), and Enhanced Puma Optimized Reinforcement Learning Algorithm (EPORLA) to real-time detection of anomalies in students’ examination results was effectively demonstrated through a custom Graphical User Interface (GUI), as shown in Figure 3 and Figure 4. This GUI enables users to load student results data, select classifiers, train the model, and visualize performance and blockchain storage. The dataset contained 6238 records, including matriculation number, programme level, course code, scores, and timestamp. To ensure robust training, 70% of the dataset was allocated for training and 30% for testing using the random sub-sampling cross-validation method, mitigating overfitting and improving the generalization ability of the models. In Figure 3, the initial stage of the GUI showcases the process of data input, classifier selection, and parameter settings like training percentage and number of epochs. After loading the dataset, the GUI displays a table of original results and sample scores. Once the training and validation process is initiated, the model attempts to identify patterns and anomalies based on the score distributions. Figure 4 presents the enhanced model evaluations using RL, PORLA, and EPORLA under increased training epochs. The Puma optimizer-enhanced RL model trained with 800 epochs achieved the best performance based on the evaluated metrics used, showing improvement in the precision-recall trade-off due to the Puma optimizer’s balance of exploration and exploitation. These improvements reflect EPORLA’s ability to adaptively fine-tune learning parameters, enhancing anomaly detection in a dynamic academic dataset. The performance table within the GUI gives a side-by-side comparison of classifier performance metrics across different epochs. Furthermore, the integration of blockchain as an unalterable storage system, as illustrated in the blockchain overview section of the GUI in Figure 4, ensures that the identified anomalies and validated records are securely logged. Each transaction block is timestamped and hashed, representing an immutable audit trail for examination result validation. This integration not only strengthens data integrity but also fosters transparency and trust in academic institutions. The system enables administrators to track alterations and verify records without compromise. Ultimately, the GUI offers a seamless and intelligent platform for real-time anomaly detection and secure result management using a hybrid of advanced machine learning and blockchain technologies. The Puma Optimizer (PO) was applied in this study to fine-tune the hyperparameters of the reinforcement learning model, specifically targeting learning rate, discount factor, exploration rate, and number of episodes. Table 1 presents the results from 30 iterations of the optimization process, with each row indicating a unique parameter combination and the corresponding objective function value. While several parameter sets yielded moderately high performance, the best result emerged at iteration 23, where the learning rate was 0.029, the discount factor was 0.979, the exploration rate was 0.106, and the number of episodes was 340. This configuration recorded the lowest objective function value of 0.017, confirming it as the optimal hyperparameter combination selected by Puma Optimizer (PO). Despite the effectiveness of Puma optimizer, some iterations exhibited high objective values (like 0.944 at iteration 29), indicating inconsistency in convergence. Selection of Optimal RL Parameters using the standard Puma Optimizer. To further enhance the tuning process, an Enhanced Puma Optimizer with Quantum Superposition Mutation (EPO-QSM) was employed, as shown in Table 2. This hybrid approach introduced quantum-inspired diversity into the optimization strategy, improving global exploration and local refinement. Selection of Optimal RL Parameters using the Enhanced Puma Optimizer with QSM. The optimization was repeated across 30 iterations using the same hyperparameter space, and iteration 10 was identified as the best configuration, yielding an objective function value of just 0.034. This configuration included a learning rate of 0.071, a discount factor of 0.884, an exploration rate of 0.296, and a total of 970 episodes. The results from EPO-QSM indicated more stable and consistent improvements in objective function values across various iterations compared to the conventional PO. Comparatively, EPO-QSM outperformed PO in achieving optimal reinforcement learning hyperparameters for the anomaly detection task. While both optimizers succeeded in identifying high-performing parameter sets, EPO-QSM demonstrated better consistency and lower overall objective values across more iterations, confirming the advantage of integrating quantum superposition mutation. This improvement can be attributed to EPO-QSM’s ability to escape local optima and better explore the solution space. The application of EPO-QSM not only refined the learning parameters but also contributed to the improved performance metrics observed in the reinforcement learning-based anomaly detection model. Consequently, this advanced optimization approach facilitates more effective real-time analysis of examination results, resulting in a highly accurate and reliable model. Performance of the Traditional RL In Table 3, evaluation across different training epochs—200, 400, 600, and 800—revealed a slight decline in True Positives (TP) from 346 to 343, while False Negatives (FN) increased from 28 to 31. Meanwhile, False Positives (FP) decreased consistently from 35 to 28, and True Negatives (TN) increased from 1462 to 1469, indicating the model’s growing accuracy in identifying legitimate records. This gradual shift in the confusion matrix components highlighted the model’s improved discrimination power as the training deepened. Performance Evaluation Results based on RL. A deeper examination of the false positive rate (FPR) confirmed the model’s increasing reliability. The FPR dropped from 2.34% at 200 epochs to 1.87% at 800 epochs, showing a reduction in incorrect anomaly detections among valid records. This was complemented by an increase in specificity—from 97.66% to 98.13%—indicating the system’s stronger ability to recognize true negatives. However, there was a marginal drop in recall, from 92.51% to 91.71%, suggesting a slight reduction in the model’s sensitivity to identifying all anomalies. Despite this, the consistently high recall values across all epochs affirmed the model’s ability to identify the majority of actual anomalous results. In terms of precision, there was a positive upward trend, increasing from 90.81% at 200 epochs to 92.45% at 800 epochs. This implied that the proportion of true anomalies among all flagged cases improved with extended training. Consequently, the F1-Score, which balances precision and recall, also improved steadily—from 94.11% to 95.21%—indicating overall enhanced classification performance. The accuracy of the RL model improved slightly, increasing from 96.63% to 96.85%, highlighting a reliable overall detection system for anomalies in real-time examination results, as shown in Table 3. Despite the improved performance metrics, detection time increased significantly with the number of epochs, from 22.23 ms at 200 epochs to 97.04 ms at 800 epochs. While the accuracy and F1-score benefited from longer training durations, the trade-off was evident in real-time application contexts where speed is critical. The slight reduction in recall, despite higher precision, also suggested the need to balance between identifying all anomalies and minimizing false alarms. Nonetheless, the reinforcement learning model remained effective and dependable for real-time anomaly detection, especially when accuracy was prioritized over processing speed. These findings demonstrated the impact of careful hyperparameter selection on the overall success of RL-based intelligent systems in dynamic academic environments. Performance of PORLA on Anomaly Detection The Puma Optimized Reinforcement Learning Algorithm (PORLA) demonstrated significant improvements in both accuracy and efficiency for real-time anomaly detection in examination outcomes. The Puma Optimizer (PO) was instrumental in selecting optimal hyperparameters such as learning rate, discount factor, exploration rate, and number of episodes, which significantly influenced the performance of the RL model. From 200 to 800 epochs, True Positives (TP) remained high, slightly decreasing from 358 to 355, while False Negatives (FN) rose marginally from 16 to 19. Similarly, False Positives (FP) decreased from 24 to 16, indicating fewer incorrect detections, while True Negatives (TN) increased from 1473 to 1481. These trends in the confusion matrix suggested that PORLA maintained a high level of consistency in accurately identifying anomalies with minimal misclassification. In terms of the false positive rate (FPR), PORLA exhibited a consistent decline from 1.60% at 200 epochs to just 1.07% at 800 epochs, underscoring its increasing ability to accurately disregard non-anomalous data. Correspondingly, the specificity improved from 98.40% to 98.93%, indicating enhanced ability in detecting genuine results without labelling them as anomalous. While there was a slight decrease in recall from 95.72% to 94.92%, it remained above 94%, showing strong sensitivity to actual anomalies. The high recall values coupled with low FPR confirmed the model’s strong generalization and balanced detection capabilities. These results underscored the robustness of PORLA in maintaining accuracy even as model training became deeper and more refined, as defined in Table 4. Evaluation Results based on PORLA. Precision also showed a steady increase from 93.72% to 95.69% as epochs progressed, indicating that most flagged results were truly anomalous. This enhancement in precision is significant for real-time anomaly detection, as it reduces false alarms and builds users’ trust in the system. The accuracy of the PORLA system steadily climbed from 97.86% to 98.13%, reflecting its comprehensive correctness across all classifications. More importantly, the F1-score, which harmonizes precision and recall, increased from 96.00% to 97.28%, marking a consistent improvement in overall performance. These performance metrics collectively validated the effectiveness of Puma optimizer-based hyperparameter tuning in optimizing reinforcement learning for critical real-time applications. Finally, in terms of detection speed, the PORLA system remained efficient with detection time rising from 18.38 ms at 200 epochs to 73.66 ms at 800 epochs—still faster compared to other models with similar training lengths. While there was a natural increase in time due to deeper learning, it remained within an acceptable range for real-time deployment. The trade-off between increased accuracy and moderate increases in computation time is favourable, especially in sensitive systems like academic result anomaly detection. The consistent improvements across metrics suggested that PORLA, guided by Puma, optimized reinforcement learning parameters, provided a powerful and reliable solution. Ultimately, the system offered a promising balance of accuracy, precision, recall, and speed, making it highly suitable for high-stakes, real-time anomaly detection tasks. Performance of EPORLA on Anomaly Detection The Enhanced Puma Optimized Reinforcement Learning Algorithm (EPORLA), which integrates Quantum Superposition Mutation (QSM) into the traditional Puma optimizer, demonstrated outstanding performance in real-time examination results anomaly detection. This enhancement significantly refined the hyperparameter selection process for reinforcement learning, including learning rate, discount factor, exploration rate, and number of episodes. True Positives (TP) showed a slight reduction from 367 at 200 epochs to 364 at 800 epochs, while False Negatives (FN) rose modestly from 7 to 10. False Positives (FP) impressively dropped from 15 to just 7, and True Negatives (TN) increased from 1482 to 1490, indicating improved classification of valid results. This trend highlighted EPORLA’s ability to maintain a high anomaly detection rate with reduced misclassification, as expressed in Table 5. In Table 5, the system’s false positive rate (FPR) decreased from 1.00% to 0.47% across the training epochs, indicating a significant reduction in false alerts and enhanced recognition of non-anomalous data. Specificity improved concurrently from 99.00% to 99.53%, emphasizing the model’s exceptional capability in correctly identifying genuine records. Although recall showed a slight decline from 98.13% to 97.33%, it remained consistently high, demonstrating the model’s reliability in capturing the majority of anomalies. The balance between high specificity and high recall indicates that EPORLA achieved both low false positives and minimal false negatives. This balance is critical in academic systems where both missed anomalies and false alarms can be costly. Evaluation Results based on EPORLA. Precision increased steadily from 96.07% to 98.11%, showing that EPORLA became more confident and accurate in its anomaly predictions as training progressed. This improvement translated into a significant rise in the F1-score, which advanced from 97.51% at 200 epochs to 98.82% at 800 epochs, representing a near-perfect harmony between precision and recall. Accuracy also saw a consistent upward trend from 98.82% to 99.09%, affirming the model’s overall correctness in decision-making. These performance gains demonstrated the advantage of enhancing the Puma optimizer with quantum-inspired mutation strategies, which effectively fine-tuned reinforcement learning configurations for optimal outcomes. Collectively, these metrics positioned EPORLA as the most accurate and reliable anomaly detection model among the three tested. Another advantage of EPORLA is the highly efficient detection time, which ranged from 11.67 ms at 200 epochs to only 42.38 ms at 800 epochs, making it significantly faster than both PORLA and the traditional RL models. The reduced computation time, combined with higher detection accuracy, made EPORLA well-suited for real-time applications where speed and precision are critical. As a result, EPORLA not only outperformed others in terms of accuracy and reliability but also proved to be the most time-efficient solution. Overall, the integration of the enhanced Puma optimizer into the reinforcement learning framework sets a new benchmark for intelligent, responsive, and accurate anomaly detection systems in educational environments. Comparison of RL, PORLA, and EPORLA Models The comparison of ordinary Reinforcement Learning (RL), Puma Optimized Reinforcement Learning (PORLA), and Enhanced Puma Optimized Reinforcement Learning (EPORLA) in real-time examination results anomaly detection revealed significant performance improvements through optimization. RL, using manually selected parameters, achieved a decent performance with a False Positive Rate (FPR) of 1.87% and specificity of 98.13%, indicating a fair ability to identify non-anomalous results. However, the recall of RL stood at 91.71%, suggesting it missed more anomalies compared to the optimized models. Precision was 92.45%, and the overall accuracy was 96.85%, while the F1-Score reached 95.21%, reflecting a moderately balanced model as analyzed in Table 6. Despite this, RL required the highest detection time of 97.04 ms, making it less efficient for real-time deployment. Evaluation of RL, PORLA, and EPORLA. When the Puma Optimizer was introduced in PORLA, it significantly enhanced the RL model by automating the selection of optimal parameters such as learning rate, discount factor, exploration rate, and number of episodes. PORLA reduced the FPR to 1.07% and increased specificity to 98.93%, minimizing the occurrence of false alerts. Sensitivity (Recall) improved to 94.92%, indicating better anomaly detection capability. Precision also rose to 95.69%, and accuracy climbed to 98.13%, with an F1-score of 97.28%, showing a well-balanced and more reliable model than the traditional RL. Detection time dropped to 73.66 ms, marking a notable improvement in processing efficiency. In Table 6, the highest performance gains were recorded with EPORLA, which further enhances the Puma optimizer through the incorporation of Quantum Superposition Mutation (QSM). QSM helped avoid premature convergence and local minima by introducing diversity in the search space, leading to the discovery of globally optimal reinforcement learning parameters. As a result, EPORLA achieved the lowest FPR of 0.47% and the highest specificity of 99.53%, showing exceptional capacity in correctly identifying legitimate examination results. Recall reached an outstanding 97.33%, with precision at 98.11%, accuracy at 99.09%, and F1-score peaking at 98.82%, the highest among all three models. Furthermore, EPORLA completed detection in just 42.38 ms, making it the fastest and most effective model for real-time anomaly detection. Discussion of the Performance Metrics The results demonstrated a clear incremental performance between the three variants of the model: The traditional Reinforcement Learning (RL) algorithm, Puma Optimized Reinforcement Learning Algorithm (PORLA), and the Enhanced Puma Optimized Reinforcement Learning Algorithm (EPORLA). As shown in Figure 5, the false positive rate (FPR) consistently decreased across epoch values for all three methods, with EPORLA achieving the lowest FPR of 0.47% at epoch 800, compared to PORLA’s 1.07% and RL’s 1.87%. This significant reduction in false positives shows that nature-inspired optimization techniques like Puma optimization can substantially improve the exploration-exploitation balance in reinforcement learning frameworks, leading to more precise classification boundaries. The enhanced algorithm incorporating Quantum Superposition Mutation further refined this capability, enabling more accurate differentiation between normal and anomalous results. Specificity results in Figure 6 revealed EPORLA’s superior performance in correctly identifying true negatives, with values rising from 99.00% at epoch 200 to 99.53% at epoch 800. PORLA achieved the second-best performance (98.93% at epoch 800), while traditional RL trailed with 98.13%. This pattern demonstrated how the integration of optimization algorithms enhanced the model’s ability to correctly classify legitimate activities. This is because optimization algorithms like the enhanced Puma optimizer can introduce adaptive parameter tuning mechanisms that allow reinforcement learning models to generalize better across diverse non-anomalous patterns. The gradual improvement across epochs indicated successful learning progression, with EPORLA’s Quantum Superposition Mutation likely contributing to its ability to escape local optima and discover more optimal decision boundaries. Figure 7 illustrates the sensitivity performance, where EPORLA again led with values ranging from 98.13% to 97.33% across epochs, followed by PORLA (95.72% to 94.92%) and RL (92.51% to 91.71%). Interestingly, all three methods exhibited a slight downward trend in sensitivity with increasing epochs, suggesting a potential trade-off between reducing false positives and maintaining true positive detection. This phenomenon aligns with the fact that when reinforcement learning agents optimize for overall accuracy, there may be slight compromises in sensitivity to achieve substantial gains in other metrics. Despite this trend, EPORLA returned the highest sensitivity throughout, utilizing its QSM to balance the precision-recall trade-off through enhanced exploration. The precision metrics shown in Figure 8 reflect steady improvement across epochs for all three variants, with EPORLA achieving the highest values (96.07% to 98.11%), followed by PORLA (93.72% to 95.69%), and RL (90.81% to 92.45%). This upward trend contrasted with the sensitivity pattern, reinforcing the precision-recall trade-off inherent in classification systems. The observed trend was because the integration of Puma optimization with reinforcement learning can create a more adaptable reward function that prioritizes precision in high-stakes detection scenarios, and which can be further enhanced by quantum-inspired mutation operators in advanced implementations. Again, EPORLA used its enhanced optimization abilities to lower false positives while maintaining strong true positive detection. Detection time results in Figure 9 revealed a significant efficiency for EPORLA, with the lowest processing times across all epochs (11.67 ms to 42.38 ms), compared to PORLA (18.38 ms to 73.66 ms) and RL (22.23 ms to 97.04 ms). This is particularly important for real-time detection systems where computational efficiency is crucial. The substantial difference between EPORLA and the other methods suggests that the QSM not only improved the accuracy but also computational efficiency. An achievement that was possible because quantum-inspired optimization components can dramatically reduce the search space exploration required in reinforcement learning, leading to faster convergence and lower computational overhead. The increasing trend across epochs for all methods reflected the growing complexity of the learned models, though EPORLA maintains the lowest slope. Finally, Figure 10 shows the overall accuracy results, with EPORLA achieving the highest values (98.82% to 99.09%), followed by PORLA (97.86% to 98.13%) and RL (96.63% to 96.85%). This comprehensive metric confirmed the superior performance of EPORLA across the testing dataset. The consistent improvement in accuracy across epochs for all methods demonstrated a successful training progression, with EPORLA maintaining its advantage throughout. EPORLA’s consistent high accuracy across epochs reinforces the fact that the synergistic combination of advanced nature-inspired optimization with reinforcement learning creates a robust framework that can adapt to complex patterns while maintaining generalization capabilities. The integration of Quantum Superposition Mutation in EPORLA appeared to have provided a significant edge in navigating the complex solution space, resulting in more optimal policy learning compared to the standard PORLA and traditional RL approaches. Discussion of Convergence Characteristic Curve Figure 11 illustrates the rate of convergence of the standard Puma Optimizer (PO) and the Enhanced Puma Optimizer (EPO) in terms of the best fitness value over 200 iterations. The graph demonstrated that EPO, which integrated Quantum Superposition Mutation (QSM), converged significantly faster than the standard PO. Within the first 30 iterations, EPO reached a near-optimal fitness value, while PO took almost twice as long to achieve a similar result. This rapid convergence of EPO is a direct consequence of QSM’s ability to introduce diversity in the solution space, thereby preventing premature convergence and ensuring a more efficient search. The superior performance of EPO is consistent across all iterations, confirming the effectiveness of QSM in enhancing the exploration and exploitation balance in the optimization process. Several authors in the literature have emphasized the importance of the convergence rate as a critical metric in evaluating the efficiency of metaheuristic algorithms. According to the authors in [34], a faster convergence rate not only signifies computational efficiency but also demonstrates the algorithm’s ability to quickly escape local optima and reach the global optimum. The faster convergence exhibited by EPO aligned with this assertion, as it reached optimal fitness levels in fewer iterations compared to PO. Comparison with an Existing Work In the realm of real-time examination results anomaly detection, the Enhanced Puma Optimized Reinforcement Learning Algorithm (EPORLA) has demonstrated superior performance compared to existing methodologies. Traditional Reinforcement Learning (RL) approaches, as discussed by researchers in [35], achieved a precision of 90.81% and a recall of 92.51% in time series anomaly detection, leading to an accuracy of 96.63%. In contrast, EPORLA recorded higher precision and recall rates, resulting in an accuracy of 99.09%. Also, authors in [23] utilized a Feed-Forward Neural Network model for the detection of result anomalies, achieving a precision of 88.92%, a recall of 96.98%, a specificity of 89.28%, and an accuracy of 92.90%. The significant improvement recorded by EPORLA over these existing techniques can be attributed to the integration of Quantum Superposition Mutation within the Puma optimizer, enhancing the selection of reinforcement learning hyperparameters and thereby optimizing the learning process as defined in Table 7. Comparison: Result of EPORLA vs. State-of-the-Art Results. Furthermore, the detection time is a critical factor in real-time systems. Studies such as those by authors in [36] and [23] explored deep actor-critic reinforcement learning and Feed-Forward Neural Network, respectively, for anomaly detection, but lacked any metric on detection time. However, EPORLA addresses this shortcoming by achieving a detection time of 42.38 ms, which is a substantial improvement over the traditional reinforcement learning method. This efficiency gain is crucial for timely interventions in examination settings, ensuring that anomalies are detected and addressed promptly.

Iteration
Learning Rate
Discount Factor
Exploration Rate
Number of Episodes
Objective Function
Best (PUMA Optimizer)
1
0.038
0.915
0.123
712
0.416
No
2
0.095
0.832
0.089
561
0.758
No
3
0.073
0.812
0.250
742
0.237
No
4
0.060
0.980
0.113
868
0.086
No
5
0.016
0.983
0.091
104
0.297
No
6
0.016
0.954
0.167
317
0.170
No
7
0.006
0.858
0.051
602
0.930
No
8
0.087
0.819
0.243
866
0.810
No
9
0.060
0.930
0.032
497
0.637
No
10
0.071
0.884
0.296
970
0.873
No
11
0.002
0.823
0.234
894
0.806
No
12
0.097
0.894
0.068
492
0.195
No
13
0.083
0.807
0.012
306
0.894
No
14
0.021
0.973
0.246
114
0.544
No
15
0.018
0.849
0.215
957
0.809
No
16
0.018
0.926
0.221
653
0.897
No
17
0.030
0.859
0.234
991
0.325
No
18
0.053
0.899
0.031
560
0.119
No
19
0.043
0.904
0.114
790
0.236
No
20
0.029
0.835
0.044
674
0.433
No
21
0.061
0.984
0.260
963
0.820
No
22
0.014
0.947
0.191
842
0.862
No
23
0.029
0.979
0.106
340
0.017
Yes
24
0.037
0.970
0.028
663
0.516
No
25
0.046
0.914
0.100
195
0.423
No
26
0.079
0.975
0.104
999
0.230
No
27
0.020
0.817
0.222
833
0.129
No
28
0.051
0.837
0.195
584
0.344
No
29
0.059
0.809
0.267
506
0.944
No
30
0.005
0.862
0.147
330
0.330
No
Iteration
Learning Rate
Discount Factor
Exploration Rate
Number of Episodes
Objective Function
Best (Enhanced PUMA + QSM)
1
0.038
0.915
0.123
712
0.417
No
2
0.095
0.832
0.089
561
0.564
No
3
0.073
0.812
0.250
742
0.294
No
4
0.060
0.980
0.113
868
0.778
No
5
0.016
0.983
0.091
104
0.770
No
6
0.016
0.954
0.167
317
0.205
No
7
0.006
0.858
0.051
602
0.400
No
8
0.087
0.819
0.243
866
0.244
No
9
0.060
0.930
0.032
497
0.231
No
10
0.071
0.884
0.296
970
0.034
Yes
11
0.002
0.823
0.234
894
0.490
No
12
0.097
0.894
0.068
492
0.405
No
13
0.083
0.807
0.012
306
0.046
No
14
0.021
0.973
0.246
114
0.227
No
15
0.018
0.849
0.215
957
0.727
No
16
0.018
0.926
0.221
653
0.196
No
17
0.030
0.859
0.234
991
0.120
No
18
0.053
0.899
0.031
560
0.394
No
19
0.043
0.904
0.114
790
0.789
No
20
0.029
0.835
0.044
674
0.197
No
21
0.061
0.984
0.260
963
0.539
No
22
0.014
0.947
0.191
842
0.611
No
23
0.029
0.979
0.106
340
0.194
No
24
0.037
0.970
0.028
663
0.584
No
25
0.046
0.914
0.100
195
0.297
No
26
0.079
0.975
0.104
999
0.508
No
27
0.020
0.817
0.222
833
0.509
No
28
0.051
0.837
0.195
584
0.431
No
29
0.059
0.809
0.267
506
0.077
No
30
0.005
0.862
0.147
330
0.669
No
Epochs
200
400
600
800
TP
346
345
344
343
FN
28
29
30
31
FP
35
33
31
28
TN
1462
1464
1466
1469
FPR
2.34
2.20
2.07
1.87
SPEC (%)
97.66
97.80
97.93
98.13
RECALL (%)
92.51
92.25
91.98
91.71
PREC (%)
90.81
91.27
91.73
92.45
ACC (%)
96.63
96.69
96.74
96.85
F1-Score (%)
94.11
94.42
94.73
95.21
Time (ms)
22.23
41.27
76.21
97.04
Epochs/Metric
200
400
600
800
TP
358
357
356
355
FN
16
17
18
19
FP
24
21
18
16
TN
1473
1476
1479
1481
FPR
1.60
1.40
1.20
1.07
SPEC (%)
98.40
98.60
98.80
98.93
RECALL (%)
95.72
95.45
95.19
94.92
PREC (%)
93.72
94.44
95.19
95.69
ACC (%)
97.86
97.97
98.08
98.13
F1-Score (%)
96.00
96.48
96.96
97.28
Time (ms)
18.38
37.31
55.06
73.66
Epochs
200
400
600
800
TP
367
366
365
364
FN
7
8
9
10
FP
15
12
9
7
TN
1482
1485
1488
1490
FPR
1.00
0.80
0.60
0.47
SPEC (%)
99.00
99.20
99.40
99.53
RECALL (%)
98.13
97.86
97.59
97.33
PREC (%)
96.07
96.83
97.59
98.11
ACC (%)
98.82
98.93
99.04
99.09
F1-Score (%)
97.51
98.00
98.49
98.82
Time (ms)
11.67
23.23
33.28
42.38
Model
RL
PORLA
EPORLA
Epochs
800
800
800
FPR
1.87
1.07
0.47
SPEC (%)
98.13
98.93
99.53
RECALL (%)
91.71
94.92
97.33
PREC (%)
92.45
95.69
98.11
ACC (%)
96.85
98.13
99.09
F1-Score (%)
95.21
97.28
98.82
Time(ms)
97.04
73.66
42.38
The Enhanced Puma Optimized Reinforcement Learning Algorithm (EPORLA) demonstrated superior performance in real-time examination results anomaly detection systems. By integrating Quantum Superposition Mutation (QSM) into the standard Puma Optimizer (PO), the enhancement significantly improved the convergence speed and global search ability of the algorithm. This led to the selection of optimal key hyperparameters such as Learning Rate, Discount Factor, Exploration Rate, and Number of Episodes, which are critical to the effectiveness of the model. The resulting system achieved outstanding performance metrics, including a reduced False Positive Rate (FPR), high Sensitivity, Specificity, and an impressive Accuracy. These results affirm the robustness and reliability of EPORLA in identifying anomalies in examination data with minimal detection time. The integration of QSM into the standard PO further allowed EPORLA to overcome sensitivity to parameter settings and the limitation of premature convergence often encountered in traditional metaheuristics when it comes to the discrete version of the optimization technique. This improvement was reflected in the high Precision and F1-Score, indicating the system’s strong balance between recall and precision. Comparatively, EPORLA consistently outperformed PORLA across all performance metrics, establishing its superiority as a more intelligent and efficient optimization framework. The reduction in detection time without compromising accuracy emphasizes EPORLA’s scalability and suitability for real-time applications. This study achieved its aim of creating a discrete and adaptable version of the Puma optimizer for reinforcement learning. Additionally, it effectively utilized the optimizer to fine-tune the hyperparameters of a reinforcement learning-based result anomaly detection model, resulting in a model highly suitable for real-time applications. In conclusion, the application of EPORLA stands as a promising approach for educational institutions seeking dependable and timely anomaly detection in examination results processing.
It is recommended that EPORLA be adopted for real-time examination results anomaly detection due to its demonstrated efficiency, accuracy, and reduced computational cost. Educational institutions and examination bodies can leverage EPORLA’s optimized reinforcement learning capabilities to automatically detect irregularities in students’ results with high precision and minimal false alarms. Future developments could explore its application in other domains of educational data mining and integrate it with machine listening for improved data integrity, transparency, and the capability to interact with its immediate auditory environment, analyze inputs, and respond with AI-guided precision.
| AI | Artificial Intelligence |
| BAD | Blockchain Anomaly Detection |
| CSV | Comma Separated Value |
| EPO | Enhanced Puma Optimizer |
| EPORLA | Enhanced Puma Optimized Reinforcement Learning Algorithm |
| FFNN | Feed-Forward Neural Network |
| FN | False Negatives |
| FP | False Positives |
| FPR | False Positive Rate |
| GB | Genesis Block |
| GRU | Gated Recurrent Units |
| GUI | Graphical User Interface |
| HMM | Hidden Markov Model |
| KNN | K-Nearest Neighbour |
| LSTM | Long Short-Term Memory |
| ML | Machine Learning |
| OCSVM | One Class Support Vector Machine |
| PO | Puma Optimizer |
| POA | Puma Optimization Algorithm |
| PoA | Proof of Authority |
| PORLA | Puma Optimized RL Algorithm |
| QSM | Quantum Superposition Mutation |
| RL | Reinforcement Learning |
| TN | True Negatives |
| TP | True Positives |
The entire research, including the formulation of the enhancement algorithm, was carried out by the main author (Y.T.). Coding and MATLAB simulation were done by O.A., Y.T., and I.A., O.I. and A.B. are full professors of computer science. They supervised the entire research. The remaining authors were involved in reviewing the manuscript and model testing.
Data for the study were obtained from the records office of Ladoke Akintola University of Technology, Ogbomoso, Nigeria. http://lautech.edu.ng (accessed on 20 March 2025).
No consent for publication is required, as the manuscript does not involve any individual personal data, images, videos, or other materials that would necessitate consent.
The authors declare no conflicts of interest regarding this manuscript.
The study did not receive any external funding and was conducted using only institutional resources.
Sincere appreciation goes to the records office of Ladoke Akintola University of Technology, Ogbomoso, Nigeria, for making available the necessary data for this study. We also appreciate the Department of Computer Science of Ladoke Akintola University of Technology, Ogbomoso, Nigeria, for providing the high-tech hardware required for the study.
[1] R. Bdiwi, C. D. Runz, S. Faïz, A. A. Chérif, "Towards a New Ubiquitous Learning Environment Based on Blockchain Technology," In IEEE 17th International Conference on Advanced Learning Technologies (ICALT), Timisoara, Romania, 2017, pp. 101–102. [CrossRef]
[2] A. Alammary, S. Alhazmi, M. Almasri, S. Gillani, "Blockchain-based Applications in Education: A Systematic Review," J. Appl. Sci., vol. 9, no. 12, 2019. [CrossRef]
[3] A. Zimek and S. Erich, Outlier Detection Encyclopedia of Database Systems, New York: Springer, 2017, pp. 1–5. Available: https://hochschulbibliographie.tu-dortmund.de/work/28885.
[4] A. Bhardwaj and S. Goundar, "A Framework for Effective Threat Detection," Netw. Secure, vol. 6, pp. 15–19, 2019. [CrossRef]
[5] K. Xun, M. Chen, I. Boukhers, "A New Evolutionary Neural Networks Based on Intrusion Detection Systems Using Multiverse Optimization," Appl. Intell., vol. 48, pp. 2315–2327, 2017. [CrossRef]
[6] X. Wang, X. Wang, M. Wilkes, A K-Nearest Neighbour Spectral Clustering-Based Outlier Detection Technique New Development in Unsupervised Outlier Detection, Heidelberg: Springer, 2021, pp. 147–172. [CrossRef]
[7] X. Xia, X. Pan, N. Li, X. He, L. Ma, X. Zhang, N. Ding, "GAN-based anomaly detection: A review," Neurocomputing, vol. 493, pp. 497–535, 2022. [CrossRef]
[8] L. Bergman and Y. Hoshen, "Classification-based anomaly detection for general data," arXiv preprint arXiv:2005.02359, , 2020. [CrossRef]
[9] J. Li, H. Izakian, W. Pedrycz, I. Jamal, "Clustering-based anomaly detection in multivariate time series data," Appl. Soft Comput, vol. 100, p. 106919, 2021. [CrossRef]
[10] G. Pang, A. van den Hengel, C. Shen, L. Cao, "Toward deep supervised anomaly detection: Reinforcement learning from partially labeled anomaly data," In 27th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Virtual Event, 2021, pp. 1298–1308. [CrossRef]
[11] M. López, B. Castejón, A. Sánchez, "Application of deep reinforcement learning to intrusion detection for supervised problems," Expert Syst. Appl., vol. 141, p. 112963, 2020. [CrossRef]
[12] M. Meyliana, Y. U. Chandra, C. Cassandra, E. Surjandy, A. E. Fernando, E. Widjaja, et al., Defying the Certification Diploma Forgery with Blockchain Platform, Lisbon: IADIS Press, 2019, pp. 63–71. [CrossRef]
[13] S. Singh and N. Singh, "Blockchain: Future of financial and cyber security," In 2nd International Conference on Contemporary Computing and Informatics (IC3I), Greater Noida, India, 2016, pp. 463–467. [CrossRef]
[14] O. S. Hamza, S. Ruqayyah, O. Mohammed, "Detecting Anomalies in Students Results Using Decision Trees," Int. J. Mod. Educ. Comput. Sci., vol. 8, no. 7, pp. 1312–1317, 2016. [CrossRef]
[15] P. A. Legg, O. Buckley, M. Goldsmith, S. Creese, "Automated Insider Threat Detection System Using User and Role-Based Profile Assessment," IEEE Syst. J., vol. 11, no. 2, pp. 503–512, 2015. [CrossRef]
[16] T. Rashid, I. Agrafiotis, J. Nurse, "A new take on detecting insider threats: Exploring the use of hidden Markov models," In 8th ACM CCS International Workshop on Managing Insider Security Threats (MIST ’16), New York, NY, USA, 2016, pp. 47–56. [CrossRef]
[17] A. Bogner, "Seeing is Understanding: Anomaly Detection in Blockchains with Visualized Features," In 2017 ACM International Joint Conference on Pervasive and Ubiquitous Computing (UbiComp ’17), Maui, HI, USA, 2017, pp. 5–8. [CrossRef]
[18] C. Goldberg, K. Strickler, A. Fremier, "Degradation and Dispersion Limit Environmental DNA Detection of Insider Threats: Increasing of Insider Threat: A Survey and Bootstrapped Prediction in Imbalanced Data," IEEE Trans. Comput. Soc. Syst., vol. 1, no. 2, pp. 135–155, 2018. [CrossRef]
[19] S. Morishima and H. Matsutani, "Acceleration of anomaly detection in blockchain using in-GPU cache," In IEEE Intl Conf on Parallel & Distributed Processing with Applications (ISPA), Melbourne, Australia, 2018, pp. 244–251. [CrossRef]
[20] S. Sirine, B. R. Sonia, C. Zièd, "Anomaly Detection Model Over Blockchain Electronic Transactions," In 15th International Wireless Communications & Mobile Computing Conference (IWCMC), Tangier, France, 2019, pp. 895–900. [CrossRef]
[21] M. Signorini, M. Pontecorvi, W. Kanoun, R. Di Pietro, "BAD: Blockchain Anomaly Detection," IEEE Access, vol. 8, pp. 173481–173490, 2020. [CrossRef]
[22] F. Sicuranza, A. Laino, M. Gribaudo, E. Reticcioli, G. Me, "A Deep Learning Approach for Detecting Security Attacks on Blockchain," In 4th Italian Conference on Cybersecurity, Ancona, Italy, 2020, pp. 212–222.
[23] S. Ziweritin, B. Baridam, U. Okengwu, "Neural Network Model for Detection of Result Anomalies in Higher Education," Sci. Africana, vol. 19, no. 2, pp. 91–104, 2020.Available: https://ajol.info/index.php/sa/article/view/200824.
[24] R. Michel and S. Rajendran, "ADOBSVM: Anomaly Detection on Blockchain using Support Vector Machine," Meas. Sens., vol. 24, p. 100503, 2022. [CrossRef]
[25] M. U. Nasir, S. Khan, S. Mehmood, M. A. Khan, M. Zubair, S. O. Hwang, "Network Meddling Detection Using Machine Learning Empowered with Blockchain Technology," Sensors, vol. 22, 2022. [CrossRef] [PubMed]
[26] J. Li, Q. Sun, F. Sun, "Enhancing Privacy-Preserving Intrusion Detection in Blockchain-Based Networks with Deep Learning," Data Sci. J., vol. 22, no. 31, pp. 1–11, 2023. [CrossRef]
[27] A. Xiong, C. Qiao, Y. Tong, B. Qi, C. Jiang, "Blockchain Abnormal Transaction Detection Method Based on Auto-encoder and Attention Mechanism," J. Supercomput., , 2023. [CrossRef]
[28] Q. Li, R. A. M. Rupam, S. Yang, Z. Xu, "Learning to Optimize for Reinforcement Learning," In 12th International Conference on Learning Representations (ICLR), Vienna, Austria, 2024. [CrossRef]
[29] J. Beauden, Mathematical optimization in neural networks enhancing the efficiency of deep learning architectures [Online], Available: https://www.researchgate.net/publication/388293946. Available online: https://www.researchgate.net/publication/388293946
[30] L. Metz, J. Harrison, C. D. Freeman, A. Merchant, L. Beyer, J. Bradbury, N. Agrawal, B. Poole, I. Mordatch, A. Roberts, "VeLO: Training Versatile Learned Optimizers by Scaling Up," arXiv preprint arXiv:2211.09760, , 2022. [CrossRef]
[31] J. Osterrieder, S. Chan, J. Chu, Y. Zhang, B. H. Misheva, C. Mare, "Enhancing Security in Blockchain Networks: Anomalies, Frauds, and Advanced Detection Techniques," arXiv preprint arXiv:2402.11231, , 2024. [CrossRef]
[32] S. Siddamsetti, C. Tejaswi, P. Maddula, "Anomaly Detection in Blockchain Using Machine Learning," J. Electr. Syst., vol. 20, no. 3, pp. 619–634, 2024. [CrossRef]
[33] M. Sadegh, S. Layeghy, M. Portmann, "Towards a Standard Feature Set of Network Intrusion Detection System Datasets," arXiv preprint arXiv:2101.11315, , 2021. [CrossRef]
[34] M. Nssibi, G. Manita, O. Korbaa, "Advances in nature-inspired metaheuristic optimization for feature selection problem: A comprehensive survey," Comput. Sci. Rev., vol. 49, p. 100559, 2023. [CrossRef]
[35] C. Zhang, J. Wang, Y. Xia, "Time series anomaly detection with reinforcement learning," arXiv preprint arXiv:2205.09884, , 2022. [CrossRef]
[36] Y. Zhong, S. Li, R. Wang, "A deep actor-critic reinforcement learning framework for anomaly detection in time series," arXiv preprint arXiv:1908.10755, , 2019. [CrossRef]
We use cookies to improve your experience on our site. By continuing to use our site, you accept our use of cookies. Learn more